Como resolver ecuaciones de primer grado

Estas empezando a descubrir las matemáticas y sus muchas formas. Con las ecuaciones se restan y suman letras ¡Quien lo iba a decir! pero tranquilo, vamos a enseñarte a resolverlas sin usar ningún aparato. Quizás, algún día necesites una calculadora de integrales, pero aun no ha llegado ese día.
¿Qué es una ecuación?
Es necesario empezar siempre por el principio ¿Acaso construyes una casa por el tejado? Si alguien te preguntara qué es una ecuación, ¿Serias capaz de contestar? Vamos a enseñarte de una manera muy sencilla
Una ecuación es una igualdad matemática, caracterizada por tener un componente desconocido, llamado incógnita.
Aquí tienes un ejemplo en donde el componente desconocido se representa con la letra X:
![]()
Por si no lo sabias, el signo igual es el actor principal en una ecuación, ya que estamos hablando de una igualdad. Los demás componentes pueden cambiar, pero el signo igual siempre va a estar ahí.
Existen ciertas ecuaciones más complicadas en donde el signo de igualdad se sustituye por un mayor o igual o un menor o igual. Eso lo veremos más adelante.
![]()
A cada una de las partes separadas por el signo igual se le llama miembro. Al lado izquierdo se le denomina primer miembro y al derecho, segundo miembro.
Hasta ahora, la explicación ha sido muy básica y es pronto para que te pierdas, así que ¡Atento!
Esta explicación es muy básica y no completamente completa, pero es bueno que te hagas una idea inicial y te familiarices con los términos.
Grado de una ecuación ¿Cómo reconocer las de primer grado?
Ya hemos visto, básicamente, lo que es una ecuación, y ahora te preguntaras ¿Cómo puedo diferenciar una ecuación de primer grado? Aja… ¡Vamos a ello!
Lo primero de todo es saber que es el grado de una ecuación, recuerda ¡El tejado de la casa se construye al final!
El grado de una ecuación coincide con el máximo exponente al que se elevan las incógnitas.
Por ejemplo, ¿Cuál sería el grado de la siguiente ecuación?

En esta ecuación, en el primer miembro tenemos la incógnita elevada a 2 y elevada a 3. En el segundo miembro la incógnita se eleva a 1. Recuerda que si la incógnita no tiene exponente significa que se eleva a 1:
![]()
Por lo tanto, la ecuación anterior es de grado 3. ¿Por qué? Porque el grado coincide con el mayor exponente de las incógnitas.
El grado de una ecuación indica el número de soluciones de la ecuación. Así, una ecuación de primer grado tiene una solución, una ecuación de segundo grado tiene dos soluciones, y así sucesivamente.
Ecuaciones de primer grado
Bueno, ya sabemos lo que es una ecuación y sabemos cómo identificar su grado. Centrémonos ahora en las ecuaciones de primer grado. ¿Por eso estas aquí, ¿verdad?
Las ecuaciones de primer grado son aquellas en las que x sólo se eleva a 1, o, en otras palabras, x aparece sola
Al ser de primer grado, solamente tiene una solución.
En general, cualquier ecuación de primer grado tiene esta forma, una vez simplificada:
![]()
Cuando no están simplificados, podemos encontrarlos con paréntesis, paréntesis, denominadores y fracciones como estos:

![]()
![]()
¿Te acaba de explotar el cerebro? Tranquilo, aprenderemos a resolverlo poco a poco, tú sigue concentrado.
Todas estas ecuaciones deben ser previamente simplificadas para poder resolverlas. Vamos a verlo, pasito a pasito.
Cómo resolver las ecuaciones de primer grado
¿Qué es resolver una ecuación?
En primer lugar, aclaremos lo que es resolver una ecuación. Resolver una ecuación es encontrar el valor numérico que x debe tener para que la igualdad sea segura.
Para ello, tenemos que simplificar la ecuación hasta dejar la x sola en uno de los miembros, que es lo que se llama aclarar o despejar la x. Lo veremos continuamente en esta y en lecciones posteriores
Para resolver ecuaciones de primer grado, se dice comúnmente que hay que borrar o despejar la x pero, ¿qué significa borrar x?
Para despejar x tenemos que pasar por una serie de pasos para reducir o simplificar la ecuación.
Para hacerlo, además de tener siempre presente la jerarquía de las operaciones, se siguen estas reglas prácticas.
Reglas prácticas para resolver ecuaciones de primer grado
Aunque es aconsejable saber cómo se transponen los términos, en la práctica se aplican estas normas prácticas:
- Cuando un término es AÑADIDO a un miembro, pasa al otro miembro RESTANDO.
- Cuando un término permanece en un miembro, pasa al otro miembro. SUMANDO.
- Cuando un término es MULTIPLICADO en un miembro, pasa al otro miembro DIVIDIENDO el miembro entero.
- Cuando un término se DIVIDE en un miembro, pasa al otro miembro MULTIPLICANDO a todo el miembro.
Los términos pueden pasar de izquierda a derecha o viceversa.
Pasos para resolver ecuaciones
Para resolver las ecuaciones de primer grado vamos a pasar por una serie de pasos:
- Reubicar los términos: Pasar los términos con x a un miembro y los números al otro miembro
- Simplificar: Agrupar términos similares
- Despejar la x
Debe quedar claro que esta no es la única forma de resolver una ecuación de primer grado. Podrías, por ejemplo, simplificar antes de reubicarte, pero la práctica te enseñará eso.
Empezaremos a resolver ecuaciones muy simples y aumentaremos la dificultad poco a poco para que lo entiendas todo.
Ejemplos de ecuaciones simples de primer grado
Veamos un ejemplo de cómo se resuelven simples ecuaciones de primer grado. Si eres capaz de comprender este tipo de ecuaciones, te resultara mucho más sencillo resolver otras ecuaciones de primer grado más complicadas (con paréntesis, denominadores, potencias...).
Partiremos de la siguiente ecuación:
![]()
Vemos que es de primer grado porque x se eleva a 1, como hemos indicado en la definición de las ecuaciones de primer grado.
Comenzamos con el primer paso
1 - Reubicar los términos.
A través de la transposición de términos, tenemos que pasar los términos que llevan x al primer miembro y los números que no llevan x al segundo miembro. Los términos que ya están en el miembro correspondiente no deben ser tocados.
Los primero de todo es fijarte en los términos con x y olvidar el resto de la ecuación.
En la ecuación original vemos que tenemos dos términos con x: 4x, que ya está en el primer miembro y -2x que está en el segundo miembro y debe ser pasado al primer miembro.
![]()
El 4x lo dejamos como está y el 2x que es RESTANDO, pasa SUMANDO al primer miembro.
![]()
Ahora vamos con los números y olvidemos el resto.
En la ecuación original teníamos dos números (términos sin x): el 14 que ya está en el segundo miembro y el +2 que está en el primer miembro y debe ser pasado al segundo miembro:
![]()
Ahora, reescribimos el primer miembro, con los términos con x ya reubicados y el 14 que ya está en el segundo miembro. Solo tienes que pasar el 2, que está SUMANDO y para que pase RESTANDO al segundo miembro
![]()
Ya hemos completado el primer paso. Ahora se encuentran los términos con x en el primer miembro y los números en el segundo.
Continuamos con el segundo paso.
2 - Simplificar: Agrupar los términos similares.
En este paso es necesario agrupar los términos similares, es decir, operar por un lado con los términos con x y por otro lado con los términos sin x.
Nunca se pueden agrupar términos con x y números, ya que no puedes operar con ellos ¡No lo olvides!
En el paso anterior, la ecuación era la siguiente:
![]()
Primero operamos con los términos de la x, y esto significa que, tienes que trabajar números delante de la x:
![]()
Ahora operamos con los números que nos quedan en el segundo término:
![]()
Eso no es más que sumar y restar números. Ponemos el primer miembro con el término ya simplificado y el resultado que obtenemos al operar el segundo
![]()
Ya tenemos los dos miembros simplificados. Para terminar, tenemos el último paso, que es borrar la x.
3 - Borrar x
Ya tenemos la ecuación con los términos en su lugar y simplificada. Ahora tendrás que despejar la x. ¡Animo, ya falta poco!
Este último paso es muy fácil y ya lo practicaste en la lección anterior, así que no debería ser un problema para ti.
Hay que dejar la x solita, y de momento tiene un 6 acompañándola.
![]()
Al multiplicar x, pasa al otro miembro que se divide:

Y ahora sólo tenemos que hacer la división:
![]()
Y esta es la solución de la ecuación. Si la fracción no es exacta, se simplifica y se deja como una fracción.
Cómo resolver las ecuaciones de primer grado con paréntesis
Para resolver las ecuaciones de primer grado con paréntesis sólo hay que añadir un paso más al procedimiento que ya conocemos para resolver las ecuaciones de primer grado:
- Eliminar el paréntesis
- Reubicar los términos: Pasar los términos con x a un miembro y los números al otro miembro
- Simplifica: Agrupar términos similares
- Despeja la x
Una vez que no tengamos más paréntesis, podemos continuar resolviendo la ecuación de primer grado de la misma manera que lo hemos hecho hasta ahora.
Veamos cómo ejecutar este nuevo paso y luego veremos ejemplos de cómo resolver ecuaciones con paréntesis.
Cómo eliminar los paréntesis en las ecuaciones de primer grado
Cuando hay paréntesis en una ecuación, significa que hay un número justo delante que está multiplicando los términos dentro del paréntesis.
Delante del paréntesis se puede encontrar: un número, un signo - o un signo +
En todos estos casos, multiplicar el número por todos los términos del paréntesis, teniendo en cuenta la regla de los signos.
Vamos con un ejemplo…
![]()
![]()
Es muy importante tener en cuenta los signos, especialmente cuando el número que multiplica el paréntesis es negativo. El proceso sería idéntico.
Puede haber un signo menos o un signo más delante del paréntesis. En ese caso equivale a multiplicar por -1 o por +1, respectivamente.
Tiene una regla más directa en ambos casos:
- Cuando hay un signo menos delante de un paréntesis, cambia de signo a los términos dentro del paréntesis
- Cuando hay un signo más delante de un paréntesis, los términos dentro del paréntesis permanecen iguales.
Ejercicios resueltos de ecuaciones de primer grado con paréntesis
Una vez que sepas como a solventar ecuaciones de primer grado con paréntesis, te darás cuenta de que todos los ejercicios se resuelven igual.
¡Un poco de practica no te va a venir mal! Vamos a resolver un ejercicio de ecuaciones de primer grado con paréntesis:
![]()
Eliminamos los paréntesis multiplicando el número que está delante por los miembros que están dentro de los paréntesis:
![]()
Nos queda una ecuación de primer grado mucho más simple, sin paréntesis, que podemos seguir resolviendo:
![]()
![]()

Al final tenemos una fracción, que hemos tenido que simplificar.
Vamos con otro ejemplo ¡No te despistes!
![]()
Tenemos este paréntesis:
![]()
Es un paréntesis con un signo menos delante. Cambiamos los signos de los términos en el interior y eliminamos el paréntesis:
![]()
Nos queda una ecuación sin paréntesis, que seguimos resolviendo como siempre:

Y para terminar, otro ejemplo:
![]()
En este caso tenemos tres paréntesis
![]()
El primero de ellos no tiene nada delante, así que lo sacamos. Los otros dos los quitamos como ya sabemos:
![]()
Una vez más, hemos eliminado todos los paréntesis y podemos seguir resolviendo la ecuación:

Cómo resolver ecuaciones de primer grado con denominadores
Las ecuaciones de primer grado con denominadores son donde se cometen la mayoría de los errores, así que presta mucha atención y no te saltes ni un paso.
Ahora voy a explicar cómo resolver las ecuaciones de primer grado con denominadores siguiendo estos pasos:
- Eliminar los denominadores
- Quitar el paréntesis
- Reubicar los términos: Pasar los términos con x a un miembro y los números al otro miembro
- Simplifica: Agrupar términos similares
- Despejar la x
Después de eliminar los denominadores, la ecuación de primer grado ya reduce en gran medida su dificultad.
En la siguiente sección, voy a explicar en detalle cómo eliminar los denominadores en la ecuación de primer grado.
Cómo eliminar los denominadores en una ecuación de primer grado
Comencemos explicando con un ejemplo cómo eliminar los denominadores.
Tenemos la siguiente ecuación:
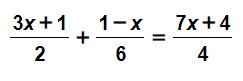
Lo primero que hay que hacer es obtener el denominador común de todos los denominadores de la ecuación, tanto del primer miembro como del segundo, ya que, al igual que con los números, para sumar y restar fracciones es necesario que tengan el mismo denominador.
En este caso, voy a elegir 24, aunque no sea el mínimo común múltiplo, por lo que verás que puedes elegir cualquier denominador, siempre que sea común. Sin embargo, es recomendable elegir siempre el mínimo, para que la ecuación sea más simple, que en este caso seria 12
Dejamos el denominador preparado y multiplicamos el numerador por su número correspondiente para obtener sus fracciones equivalentes.
Este número se obtiene dividiendo el denominador común por el denominador de la fracción original, tal como se hace cuando se opera sólo con números.

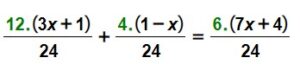
En cada miembro, colocamos todo en una sola fracción, cuyo numerador es la suma o la resta de todos los numeradores.
En este punto, podemos eliminar el denominador directamente. Hacer esto es similar a lo que sucede con la transposición de términos. Podemos multiplicar ambos miembros por el denominador común, lo que equivale a eliminarlos:

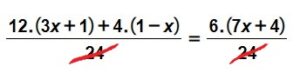
![]()
Nos queda una ecuación de primer grado con paréntesis.
Seguimos eliminando paréntesis y terminamos resolviendo la ecuación de primer grado:
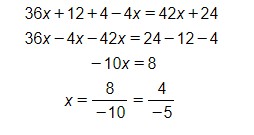 Cuyo resultado es en forma de una fracción que hemos tenido que simplificar.
Cuyo resultado es en forma de una fracción que hemos tenido que simplificar.
Al final, siempre se resuelve de la misma manera y es repetir el método una y otra vez. Cuando hayas resuelto algunas, no tendrás ningún problema.
Para que consigas más soltura, vamos a ir con otro ejemplo de ecuaciones de primer grado con denominadores.
Ejemplo de ecuaciones de primer grado con denominadores paso a paso
Las ecuaciones de primer grado con denominadores están llenas de "trampas" que hay que tener en cuenta para resolverlas bien. Por eso vamos a repetir otro ejemplo para repasar todo el procedimiento una vez más, paso a paso y aprenderlo bien.
Vamos con el primer ejemplo:

Obtenemos un denominador común y multiplicamos los denominadores con los números correspondientes para transformar a sus fracciones equivalentes la ecuación original:

Agrupamos en una sola fracción para cada miembro y eliminamos los denominadores:

Elimina los paréntesis y termina de resolver la ecuación:

En este caso la fracción no puede ser simplificada, por lo que ya estaría completada mi pequeño Jedi de las matemáticas.
Ejemplo de cómo resolver ecuaciones de primer grado con fracciones y paréntesis
Veamos cómo resolver ecuaciones de primer grado con fracciones y paréntesis. Por ejemplo, esta ecuación:

Primero operamos dentro de los paréntesis para quitar el paréntesis. Para ello, recordamos que el número multiplica cada uno de los términos del paréntesis:

Ahora operamos entre corchetes agrupando términos similares:
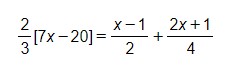
Eliminamos los corchetes multiplicándolos por la fracción. Recuerda que las fracciones han de ser multiplicadas en línea. Los términos entre corchetes tienen como denominador 1.

Tenemos términos con diferente denominador. Eliminamos los denominadores, obteniendo previamente un denominador común y calculando sus fracciones equivalentes:
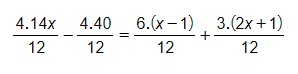
Ahora podemos eliminar los denominadores. Nos queda esta ecuación:
![]()
Seguimos eliminando los paréntesis:
![]()
Si tenemos un signo menos precediendo a una fracción cuyo numerador tiene más de un término, recuerda que el signo menos afecta a todos los términos del numerador.
Ya no tenemos paréntesis o denominadores. El siguiente paso es llevar todos los términos con x al primer miembro y los términos sin x al segundo:
![]()
Agrupamos los términos:
![]()
Y despejamos la x:
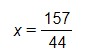
Nos ha quedado como solución una fracción que no puede ser simplificada.
Estos son los pasos para resolver ecuaciones de primer grado con denominadores y paréntesis. La dificultad dependerá de cada ecuación.
Cómo resolver ecuaciones de primer grado con fracciones
Ahora explicaré cómo se resuelven las ecuaciones de primer grado con fracciones, paso a paso.
Se llaman ecuaciones de primer grado con fracciones porque la mayor parte de sus términos son fracciones, con un solo término en el denominador, y esta es la diferencia con las ecuaciones de primer grado con denominadores, en las que los numeradores tienen dos o más términos.
En una ecuación de primer grado con fracciones, podemos encontrar una fracción que está multiplicando un paréntesis.
El paréntesis nos impide quitar los denominadores, así que lo primero va a ser eliminar el paréntesis que se multiplica por una fracción.
Estos son los pasos para resolver este tipo de ecuaciones:
- Eliminar los paréntesis multiplicados por fracciones
- Eliminar los denominadores
- Quitar el paréntesis
- Reubicar los términos: Pasar los términos con x a un miembro y los números al otro miembro
- Simplifica: Agrupar términos similares
- Despeja la x
Una vez que ya no tenemos esos paréntesis, los denominadores pueden ser eliminados normalmente y podemos seguir resolviendo la ecuación sin problemas.
Ejemplo de cómo resolver ecuaciones de primer grado con fracciones
Veamos con un ejemplo cómo se resuelven las ecuaciones de primer grado con fracciones paso a paso:
Como hemos comentado antes, podemos tener fracciones que se multiplican entre paréntesis y que debemos eliminar antes de eliminar los denominadores.
Para aprenderlo, vas a seguir este ejemplo, poco a poco. A continuación, tenemos una ecuación de primer grado con fracciones. Los numeradores tienen un solo término:
 En el que tenemos una fracción que se multiplica hasta un paréntesis:
En el que tenemos una fracción que se multiplica hasta un paréntesis:

Debemos empezar por borrar ese paréntesis porque si no lo hacemos, no es posible eliminar los denominadores.
Recordemos que cuando dos fracciones se multiplican, se multiplican en línea, es decir, el numerador por el numerador y el denominador por el denominador.
Siguiendo el ejemplo, multiplicamos el paréntesis y luego operamos con los denominadores:

Ya hemos eliminado ese paréntesis. Ahora podemos eliminar los denominadores como si fuera una ecuación de primer grado con denominadores.
El denominador en común de 2,4,5 6 6 es 30
m.c.m (2,3,5,6) = 30

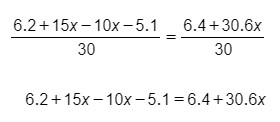 Y ahora que no tenemos denominadores, operamos con los términos, los reubicamos y despejamos la x como se explica en la lección sobre cómo resolver una ecuación de primer grado:
Y ahora que no tenemos denominadores, operamos con los términos, los reubicamos y despejamos la x como se explica en la lección sobre cómo resolver una ecuación de primer grado:

En este caso el resultado no puede ser simplificado, pero debes hacerlo siempre que sea posible.
Este es proceso a seguir para resolver las ecuaciones de primer grado con fracciones.
Ahora, y como colofón, voy a contarte 5 truquitos para resolver ecuaciones de primer grado mas rápido, para que seas el primero de la clase.
5 trucos para resolver fácilmente las ecuaciones de primer grado
Tanto en la vida diaria como en las matemáticas, existen ciertos trucos para poder hacerlo todo más fácil y rápido. Voy a mostrártelos ¡No te rindas aun, que ya falta muy poco!
Ten en cuenta que, para hacer un mejor uso de estos trucos, necesitas saber cómo resolver las ecuaciones de primer grado.
Antes de empezar, tengo que dejarte claro que para hacerlos tienes que estar seguro de que sabes lo que haces y por qué lo haces. Si tienes dudas, es preferible que no las tengas.
Vamos con ellos:
Los términos repetidos pueden ser tachados
Cuando un término se repite exactamente igual en los dos términos, podemos tachar esos términos.
Por ejemplo, en esta ecuación:
![]()
Vemos que el -3x se repite en los dos miembros:
![]()
Bueno, cuando esto ocurra, podemos tacharlos directamente y borrarlos de la ecuación.
![]()
Porque cuando reordenamos los términos, entre ellos, el resultado es 0:

Este es uno de los trucos más útiles para resolver ecuaciones, porque eliminamos los términos antes de operar con ellos y simplificamos la ecuación.
Se pueden tachar los signos menores que afectan a todo el miembro
Como en el punto anterior, si tenemos un signo menos que afecta a todo el miembro, puede ser tachado.
Pero es muy importante que afecte a todo el término, de lo contrario estaríamos modificando la ecuación original.
Por ejemplo, en esta ecuación tenemos un signo menos en cada miembro, que afecta a todo el miembro:
![]()
Por lo tanto, podemos tacharlo y los nuevos miembros siguen siendo positivos:
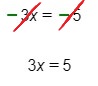
Al borrar la x, habría una fracción positiva
Se puede tachar porque si le pasamos -3 al otro miembro que está dividiendo, los signos menos al dividir dan un signo positivo por la regla de los signos:

Es importante destacar que es necesario que el signo menos afecte a todo el miembro para poder utilizar este truco. Por ejemplo, en esta ecuación no sería posible tachar los signos de menos:
![]()
Porque los signos menores sólo afectan a un término.
Para que afecten a todo el miembro, necesitaríamos un paréntesis, como en este caso:

Los denominadores que afectan a todo el miembro pueden ser tachados
Con los denominadores, tenemos el caso de que el mismo denominador divide a todo el primer miembro y a todo el segundo miembro:

En este caso, también podemos tachar los denominadores para eliminarlos:

Podemos hacerlo porque si pasamos uno de los 4 multiplicadores al otro miembro, al final se anularían entre sí como equivalente a multiplicar por 1 al segundo miembro y nos quedaríamos con una ecuación sin denominadores.

No olvides que es absolutamente necesario que el denominador afecte a todo el miembro.
Podemos pasar lo desconocido al otro miembro para que sea positivo
Otra forma de eliminar el signo menos delante de la x. Veámoslo con este ejemplo:
![]()
En lugar de pasar el -1 que multiplica x, podemos tratar -x como un término que se resta del primer miembro y pasarlo sumando al segundo miembro:
![]() Ahora, para borrar la x, pasamos 2 al primer miembro, que es la suma y la resta:
Ahora, para borrar la x, pasamos 2 al primer miembro, que es la suma y la resta:
![]()
Al final, podemos intercambiar los miembros del lugar:
![]()
No hay que confundirlo con los términos transitorios. Lo único que se ha hecho es sustituir un miembro por otro, pero el signo de los términos no varía.
El signo menos en una fracción pertenece a la fracción entera
Aunque este truco no se trata sólo de ecuaciones, pensé que sería útil recordarlo para hacerlo más claro
Hay veces en que no se sabe si el signo menos se coloca en el numerador o en el denominador. ¡Da igual!
Aunque el signo menos pertenece al numerador o al denominador, al final la fracción es negativa y el signo menos se puede colocar delante de la fracción:

Y hasta aquí esta lección, seguro que ahora ya sabes como resolver ecuaciones de primer grado en todas sus variantes, y encima conoces algunos trucos para hacerlo como un auténtico matemático.
Si te a gustado y sobre todo, te ha ayudado, deja un comentario un poco más abajo, la satisfacción que nos produce es ¡¡BRUTAL!!
-
Pingback: ¿Qué es el Teorema de Pitágoras y cómo se resuelve? - Mi apunte escolar
