Vectores: tipos, características, explicación...
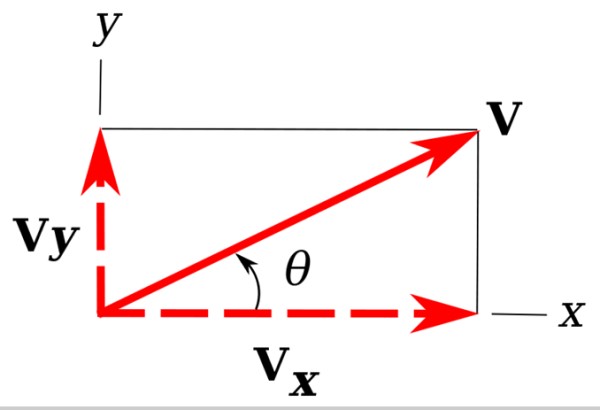
¿Sabes qué son los vectores? Antes de explicar un poco más acerca de este interesante tema, es importante que conozcas su definición en matemáticas y física. Un vector es aquel que se representa mediante un segmento que posee tres elementos: módulo, dirección y sentido. Este término proviene del latín vector que significa vectoris y traducido es transportar o conducir.
Vectores aplicados en la vida cotidiana
Su aplicación en la vida cotidiana se evidencia en la ingeniería, en el mundo real el vector es tridimensional, esto quiere decir, que existe una gran cantidad de magnitudes en el mundo real que son vectoriales y sumamente necesarios para modelar la realidad matemáticamente.

En física, se pueden evidenciar casi en un 100 % desde que comienza el desplazamiento vectorial y la mayor parte de las magnitudes deriva de la velocidad y fuerza.
Los vectores y fuerza neta, suele ocurrir que con frecuencia actúan diferentes fuerzas. Puede ser complejo cuando se calcula por separado el efecto de cada uno. Sin embargo, cada una de las fuerzas son vectores para que sean una fuerza resultante, lo que permite determinar el comportamiento de un cuerpo.
Otros casos de la vida diaria son cuando caminas, al salir de un punto de partida, saliendo de tu casa y decides ir al supermercado, allí encontrarás grados hacia donde te dirigirás y la magnitud será la distancia recorrida desde el punto de partida.

Tipos de vectores
Ten en cuenta que un vector es un segmento de una línea recta que posee módulo, dirección y sentido, en resumen, es un elemento que pertenece a un espacio vectorial. Además, se puede representar en el plano cartesiano a través de un conjunto de coordenadas (x, y) o en un sistema ortogonal (x, y, z). Es importante destacar que se representa de forma típica por medio de la fecha dibujada que se encuentra por encima del símbolo planteado.
Se clasifican según la ubicación de su punto de aplicación, en:
Vectores libres: son los que no poseen un punto de aplicación particular. En forma analítica, son aquellos que tienen las mismas componentes, y por ende, por definición son equipolentes.
a=b=c= (3,2)
En conclusión, se denomina un vector libre al conjunto de vectores equipolentes a uno dado. Aunque, cabe destacar que éste no es un vector, sino que comprende un conjunto infinito de vectores siendo todos equivalentes entre sí, y que cada vector de un vector libre es representante de éste.
Cuando se representan en un plano cartesiano es posible cualquier punto en sus orígenes. Por ello, se ubican con su origen en el origen del plano cartesiano.
Vectores fijos o ligados: son los que no poseen un determinado y único punto de aplicación. Además, cada uno de ellos componen un vector libre que representa este vector. Esto significa que AB representa el vector libre que está formado por los vectores equipolentes al vector fijo AB.
También![]() es un segmento de recta orientado que queda determinado por un punto de origen, A (a1, b1), y un punto extremo B (a2, b2). Las coordenadas del punto de origen, A (a1, b1), y del punto de extremo B (a2, b2), determinan las componentes: (a2-a1, b2- b1) vector fijo AB
es un segmento de recta orientado que queda determinado por un punto de origen, A (a1, b1), y un punto extremo B (a2, b2). Las coordenadas del punto de origen, A (a1, b1), y del punto de extremo B (a2, b2), determinan las componentes: (a2-a1, b2- b1) vector fijo AB
Vectores deslizantes: se encuentran en una misma recta directriz sin tener en común un punto de aplicación, además tienen igual dirección, módulo y sentido.
Vectores angulares o concurrentes: debido a que atraviesan un mismo punto forman un ángulo, por ello también se llaman angulares.
Vectores colineales: son aquellos que aparecen en la misma recta, además pueden ser paralelos a una recta.
Vectores coplanarios: son aquellos cuyas rectas de acción se sitúan en el mismo plano.
Vectores equipolentes: Se dice que dos vectores son equipolentes si coinciden en dirección, módulo y sentido, como los vectores ![]() y
y ![]()
Explicación de tipos de vectores y ejemplos
Equipolentes
¿Sabes cuándo dos vectores son equipolentes? Como pudiste ver en los tipos de vectores, dos vectores son equipolentes si coinciden en dirección, módulo y sentido, como los vectores ![]() y
y ![]()
Por ejemplo, cuando se traslada un vector en el plano se obtienen vectores equipolentes, es decir, el vector generado después de la traslación es equipolente al vector original. También es importante destacar que todo vector en el plano se puede representar con un vector equipolente en el origen de coordenadas, esto significa que todo par de vectores equipolentes poseen las mismas componentes.
Ejemplo:
Dados los puntos A (0,1), B (3,4), C(3,0) y D (6,3); los vectores ![]() y
y ![]() tienen las mismas componentes, por tanto, son equipolentes ya que:
tienen las mismas componentes, por tanto, son equipolentes ya que:
Las componentes de ![]() son
son ![]() = (3-0, 4-1) = (3,3)
= (3-0, 4-1) = (3,3)
Las componentes de ![]() son
son ![]() = (6-3, 3-0) =(3,3)
= (6-3, 3-0) =(3,3)
Opuestos, paralelos y ortogonales
Un conjunto de dos o más vectores pueden tener una posición relativa con respecto a otro, estos pueden ser ortogonales, paralelos u opuestos. A continuación, aquí tienes la explicación de cada uno de ellos:
Vectores opuestos: si tienen sentidos opuestos y tienen la misma dirección. Todo vector ![]() posee su vector opuesto, y se denota:
posee su vector opuesto, y se denota: ![]() y posee las siguientes componentes:
y posee las siguientes componentes: ![]()
Vectores paralelos: si las rectas que describen las direcciones son paralelas, entonces los vectores son paralelos.
Vectores ortogonales: si se forma un ángulo de 90°, entonces son ortogonales.
Ejemplo
Determina si los valores ![]() y
y ![]() son ortogonales si las componentes vienen dadas por
son ortogonales si las componentes vienen dadas por ![]() y
y ![]()
Solución:
En primer lugar procede a determinar el ángulo que forma cada vector con el eje x, se puede determinar si entre ellos se forma un ángulo de 90°
![]() , por lo tanto
, por lo tanto ![]()
![]() , por lo tanto
, por lo tanto ![]()
Por lo tanto, se concluye que los vectores son ortogonales, debido a que el ángulo que se forma entre ellos es de 90°
Unitario
Se llama vector unitario debido a que cumple con la condición de tener la unidad como módulo, esto significa que ![]() es unitario si se cumple que:
es unitario si se cumple que: ![]() =1
=1
A continuación, aquí tienes la representación de un vector unitario en el plano cartesiano:
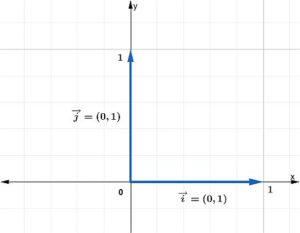
Nulo
Por otra parte, un vector se llama nulo, cuando ambas componentes del vector son igual a cero, esto indica que el módulo de dicho vector es 0. En otras palabras se define como el vector tiene como punto de origen y extremo son iguales.
Ejemplo:
0=0i+0j
Este es el único en el que la longitud es cero, como se puede ver a continuación:
![]()
Componentes de un vector
Los vectores generalmente se denotan con letras mayúsculas que señalan los puntos de origen y extremo en el plano, por ejemplo ![]() en este caso, el vector
en este caso, el vector ![]() indica que el punto de origen es A y el punto B es el extremo. También se pueden representar utilizando letras minúsculas de la siguiente manera:
indica que el punto de origen es A y el punto B es el extremo. También se pueden representar utilizando letras minúsculas de la siguiente manera: ![]() ,
, ![]() ,
, ![]() ,...
,...
Cabe destacar que todo vector ![]() en el plano cartesiano viene determinado por los puntos de origen
en el plano cartesiano viene determinado por los puntos de origen ![]() y extremo
y extremo ![]() se puede expresar como un vector
se puede expresar como un vector ![]() que posee una componente horizontal
que posee una componente horizontal ![]() y una componente vertical
y una componente vertical ![]()
Si deseas determinar las componentes del vector ![]() en el que el origen no es el del plano cartesiano, se deben restar las coordenadas del punto extremo
en el que el origen no es el del plano cartesiano, se deben restar las coordenadas del punto extremo ![]() , menos la coordenada del punto de origen
, menos la coordenada del punto de origen ![]() de la siguiente manera:
de la siguiente manera:
![]()
Ejemplo:
Si el vector ![]() tiene como punto extremo B (7,7) y como origen el punto A (4,2) se tiene que la componente de
tiene como punto extremo B (7,7) y como origen el punto A (4,2) se tiene que la componente de ![]() es:
es:
![]()
![]() = (7-4, 7-2)
= (7-4, 7-2)
![]() = (3, 5)
= (3, 5)
Entonces, la componente del ![]() = (3, 5)
= (3, 5)
Características de los vectores
Como bien sabes un vector fijo está representado por dirección, longitud y sentido, en el que la longitud es proporcional a su valor numérico, de nombre módulo. Otras de las características de los vectores son:
La dirección del vector fijo AB se conoce como la recta que pasa por A y B.
Sentido: el sentido del vector fijo AB se define sobre la recta determinada por A y B cuando lo trasladamos de A a B, es decir, lo que marca la flecha del vector, y su segmento tiene dos posibles sentidos opuestos.
El módulo o longitud del vector AB, es la longitud del segmento orientado AB. Se representa por: también se puede escribir como AB
Para calcular el módulo se calcula el teorema de Pitágoras o la ecuación de la distancia entre dos puntos:
![]()
Ejemplo:
Dados los vectores:
A (3,4)
B (5,7)
![]()
![]()
![]()
![]()
![]()
Adición y sustracción de vectores
La adición de vectores consiste en la resolución de operaciones entre los vectores que tienen como resultado un solo vector. Además, también resaltaremos el método geométrico y el método del paralelogramo.
Es importante tener en cuenta que para sumar dos o más vectores deberás tener en cuenta el traslado de los vectores, para ello, el extremo del primero deberá coincidir con el extremo del segundo, y el primer extremo del origen coincida con el extremo del segundo. Finalmente, resultará un solo vector.
Ejemplo:
Dado los siguientes vectores:
![]() ,
, ![]() , determine:
, determine: ![]() =?
=?
Pasos para resolver la adición de vectores, se procede de la siguiente manera:
- En primer lugar organiza las suma
 sustituyendo ambos
sustituyendo ambos - Seguidamente, procede a sumar la primera componente "x" con la segunda componente "x", después sumar la primera componente "y" con la segunda componente "y"
![]() = (4+3, 6+5)
= (4+3, 6+5)
![]() = (7, 11)
= (7, 11)
Método geométrico
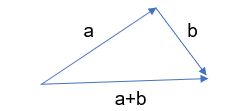
Considerando dos vectores libres a y b como se observa en la siguiente figura:
El vector obtenido le llamaremos el vector suma de los vectores a y b, que se denota a+b
Método del paralelogramo
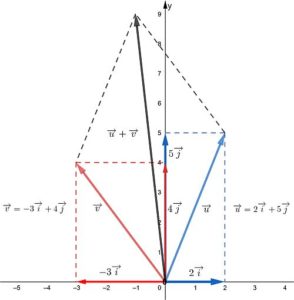
Consideramos nuevamente los dos vectores libres a y b., debido a que del origen de a se construye un vector equipolente al vector b. Por el extremo de a se traza una paralela al vector b y por el extremo de b se dibuja el vector a.
Luego, se dibuja un vector sobre la diagonal del paralelogramo, que tiene origen en el origen de los vectores y su extremo en el punto en el que se cortan las paralelas. Este vector se llama suma de a y b.
La sustracción o resta de vectores es una operación que se realiza con dos segmentos. Para realizar la operación lo que debes hacer es tomar un vector y sumar su opuesto.
Dados vectores ![]() en el plano cartesiano, la diferencia a menos b, queda de la siguiente manera:
en el plano cartesiano, la diferencia a menos b, queda de la siguiente manera:
![]() (x1, y1) + (-x2, -y2)
(x1, y1) + (-x2, -y2)
![]() (x1- x2, y1 -y2)
(x1- x2, y1 -y2)
Ejemplo:
Se desea hallar la diferencia a-b, siendo a= (-3, 4) y b= (5,-2)
![]() (-8, 7) – (5,-2)
(-8, 7) – (5,-2)
![]() [-8-5, 7-(-2)]
[-8-5, 7-(-2)]
![]() (-13, 9)
(-13, 9)
Propiedades de la adición de los vectores
Propiedad conmutativa
Para aplicar la propiedad conmutativa deberás tener en cuenta que el orden de los sumandos no altera la suma. Es decir, para el par de vectores a y b se cumple:
![]()
Ejemplo # 1
Pasos para aplicar la propiedad conmutativa
1. En primer lugar deberás identificar los vectores a y b
2. Luego, procedes a igualar a y b, aplicando la propiedad conmutativa.
3. Posteriormente, resuelves la operación aritmética.
4. Por último, asegúrate que los resultados son iguales.
a=(2,3) b=(4,-1)
[2+4, 3+(-1)] = (4+2, -1+3)
(6,2) =6,2)
Propiedad asociativa
Al sumar dos o más vectores de distintas formas se obtiene el mismo resultado. Dados los vectores a, b y c, se cumple:
(a+b) +c= a+(b+c)
Pasos para aplicar la propiedad asociativa
1. En primer lugar deberás identificar los vectores a, b y c
2. Luego, procedes a sustituir a, b y c en la fórmula de la propiedad asociativa.
3. Posteriormente, resuelves la operación aritmética en ambos lados
4. Por último, asegúrate que los resultados sean iguales, de no ser así, deberás revisar las operaciones realizadas.
Ejemplo
a=(2,3); b=(4,-5); c= (3,2)
[(2,3) +(4,-5)] +(3,2) = (2,3) +[(4,-5)+(3,2)]
[(2+4, 3+(-5)] +(3,2)= (2,3) + [(4+3, -5+2)]
[6,-2]+ (3,2)= (2,3)+[7,-3]
(6+3, -2+2)= (2+7, 3+(-3))
(9,0)= (9,0)
Inverso aditivo
Cada vector a tiene un opuesto, que se representa como -a, lo que demuestra: a+(-a) =0
Producto de un número real por un vector
La multiplicación o producto de un número real por un vector viene dado por un número real θ por ![]() , que resulta θ
, que resulta θ![]() , es decir, posee:
, es decir, posee:
- La misma dirección que
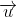
- Posee igual módulo de
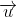 por el valor absoluto de θ
por el valor absoluto de θ
Ejemplo:
Si ![]() =(5,-2) y θ= 4, entonces:
=(5,-2) y θ= 4, entonces:
θ![]() = 4. (5,-2)
= 4. (5,-2)
θ![]() =(20, -8)
=(20, -8)
Determinar 3. ![]() , siendo
, siendo ![]() = (2,6)
= (2,6)
3.![]() = 3. (2,6)
= 3. (2,6)
3![]() = (6,18)
= (6,18)
Módulo de un vector
La longitud de ![]() se conoce como módulo, denotado así:
se conoce como módulo, denotado así: ![]() Al observar en un plano cartesiano las componentes del
Al observar en un plano cartesiano las componentes del ![]() corresponden a las proyecciones que son perpendiculares del vector sobre los ejes del plano cartesiano, por lo que al observar en un triángulo rectángulo la hipotenusa
corresponden a las proyecciones que son perpendiculares del vector sobre los ejes del plano cartesiano, por lo que al observar en un triángulo rectángulo la hipotenusa ![]() y los catetos son las componentes del vector.
y los catetos son las componentes del vector.
Al aplicar el teorema de Pitágoras a un triángulo rectángulo se observa la siguiente expresión si se desea determinar el módulo si se conocen sus componentes.
![]()
Puedes utilizar esta fórmula para determinar las componentes del vector si tiene el módulo y la otra componente.
Ahora que conoces más acerca de vectores, definición, tipos y características es recomendable que practiques ejercicios para reforzar tus conocimientos.

Deja una respuesta